Twelve Days 2013: Sensor Fusion

Day Seven: Sensor Fusion

TL/DR

Sensor fusion is a generic term for techniques that address the issue of combining multiple noisy estimates of state in an optimal fashion. There’s a straight forward view of it as the gain on a Kalman–Bucy filter, and an even simpler interpretation under the central limit theorem.

A Primer on Stochastic Control

Control theory is one of my favorite fields with a ton of applications. As the saying goes, “if all you have is a hammer, everything looks like a nail,” and for me I’m always looking for ways to pose a problem as a state space and use the tools of control theory. Control theory gets you everything from cruise control and auto pilot to the optimal means of executing an order under some set of volatility and market impact assumptions. The word “sensor” is general and can mean anything that produces a time series of values—it need not be a physical one like a GPS or LIDAR, but it certainly can be.

Estimating state is a pillar of control theory; before you can apply any sort of control feedback you need to know both what your system is currently doing and what you want it to be doing. What you want it to do is a hard problem in and of itself as the what requires you to figure out an optimal action given your current state, the cost of applying the control, and some (potentially infinite) time horizon. The currently doing part isn’t a picnic either as you’ll usually have to figure out “where you are” given a set of noisy measurements past and present; that’s the problem of state estimation.

The Kalman filter is one of many approaches to state estimation, and the optimal one under some pretty strict and (usually) unrealistic assumptions (the model matches the system perfectly, all noise is stationary IID Gaussian, and that the noise covariance matrix known a priori). That said, the Kalman filter still performs well enough to enjoy widespread use, and alternatives such as particle filters are computationally intensive and have their own issues.

Sensor Fusion

Awhile back I discussed the geometric interpretation of signal extraction in which we addressed a similar problem. Assume that we have two processes generating normally distributed IID random values, $X = (\mu_1, \sigma_1)$ and $Y = (\mu_2, \sigma_2)$. We can only observe $Z = X + Y$, but what we want $X$, so the best that we can do is $\E[X | Z = c]$. As it turns out the solution has a pretty slick interpretation under the geometry of linear regression. Sensor fusion addresses a more general problem: given a set of measurements from multiple sensors, each one of them noisy, what’s the best way to produce a unified estimate of state? The sensor noise might be correlated and/or time varying, and each sensor might provide a biased estimate of the true state. Good times.

Viewing each sensor independently brings us back to the conditional expectation that we found before (assuming that the sensor has normally distributed noise of constant variance). If we know the sensor noise a priori (the manufacturer tells us that $\sigma = 1m$ on a GPS, for example) it’s easy to compute $\E[X | Z = c]$, where $X$ is our true state, $Y$ is the sensor noise, and $Z$ is what we get to observe. In this context it’s easy to see that we could probably just appeal to the central limit theorem, average across the state estimates using an inverse variance weighting, and call it a day. Given that we have a more detailed knowledge of the process and measurement model, can we do better?

A Simple Example

Let’s consider the problem of modeling a Gaussian process with $\mu = 100$ and $\sigma = 2$. We have three sensors with $\sigma_1 = .6$, $\sigma_2 = .7$, and $\sigma_3 = .8$. Sensor one has a correlation of $r_{12} = .3$ with sensor two, a correlation of $r_{13} = .1$ with sensor three, and sensor two has a correlation of $r_{23} = .1$ with sensor three. Assume that they have a bias of .1, -.2, and 0, respectively.

Our process and measurement models are $\dot{x} = Ax + Bu + w$ with $w \sim N(0, Q)$ and $y = Cx + v$ with $v \sim N(0, R)$, respectively. For our simple Gaussian process that gives:

From there we can use the dse package in R to compute our Kalman gain state estimate via sensor fusion. In many cases we would need to estimate the parameters of our model. That’s a separate problem known as system identification and there are several R packages (dse included) that help with this. Since we’re simulating data and working with known parameters we’ll skip that step.

require(MASS)
require(dse)
require(reshape2)
require(ggplot2)

samples <- 1000
q <- 2
z0 <- 100
sigma1 <- .6
sigma2 <- .7
sigma3 <- .8
r12 <- .3
r13 <- .1
r23 <- .2
bias1 <- .1
bias2 <- -.2
bias3 <- 0
R <- matrix(nrow = 3, ncol = 3)
R <- rbind(c(sigma1^2, r12 * sigma1 * sigma2, r13 * sigma1 * sigma3),
			c(r12 * sigma1 * sigma2, sigma2^2, r23 * sigma2 * sigma3),
			c(r13 * sigma1 * sigma3, r23 * sigma2 * sigma3, sigma3^2))


path <- z0 + cumsum(rnorm(samples, mean = 0, sd = q))
observed <- path + mvrnorm(n = samples, c(bias1, bias2, bias3), R)

ss.model <- SS(F = as.matrix(1), Q = as.matrix(q^2),
	H = as.matrix(c(1, 1, 1)), R = R, z0 = z0)
smoothed.model <- smoother(ss.model, TSdata(output = observed))
state.est <- smoothed.model$smooth$state

rmsd <- function(actual, estimated) {
    sqrt(mean((actual - estimated)^2))
}

est.rmsd <- c(rmsd(path, state.est),
	apply(observed, 2, function(x) rmsd(path, x)))

Plotting the first 50 data points gives:

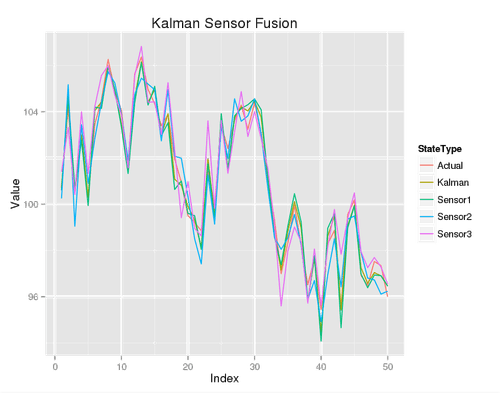
It’s a little hard to tell what’s going on but you can probably squint and see that the fusion sensor is tracking the best, and that sensor three (the highest variance one) is tracking the worst. Computing the RMSD gives:

• Kalman: .49
• Sensor 1: .59
• Sensor 2: .71
• Sensor 3: .79

Note that the individual sensors have an RMSD almost identical to their measurement error. That’s exactly what we would expect. And, as we expected, the sensor fusion estimate does better than any of the individual ones. Because our sensor errors were positively correlated we made things harder on ourselves. Re-running the simulation without correlation consistently gives a Kalman RMSD of $\approx .40$. How did the bias impact our simulation? Calculating $\text{bias} = \bar{y - \hat{y}}$ gives:

• Kalman: -.04
• Sensor 1: -.08
• Sensor 2: .22
• Sensor 3: .003

The Kalman filter was able to significantly overcome the bias in sensors one and two while still reducing variance. I specifically chose the bias-free sensor as the one with the most variance to make things as hard as possible. This helps to illustrate one very cool property of Kalman sensor fusion—the ability to capitalize on the bias-variance trade-off and mix biased estimates with unbiased ones.